GPU Benchmarks
Eric Bainville - Nov 2009Addition
Representing large numbers, and the Avizienis algorithm
The conventional base B representation of numbers requires sequential processing for carry/borrow propagation, and is not suited for massively parallel algorithms.
We will use a Avizienis representation [1] to get rid of carry propagation. An integer X is represented by a vector of N digits xi, such that X=Σ xi Bi, i=0..N-1. The difference with the standard notation is that the digits xi are no more constrained to be in [0,B-1], but can take any value in an interval [-M,M]. If M is chosen large enough (2M+1>B), any integer in -L..L can be represented, where L=Σ M Bi, i=0..N-1. With 2M+1>B, the representation is not unique. Using this redundancy, we will see how carry propagation can be "absorbed" in the next digit, and does not need to be propagated further. For more details on number representations, see for example the 2nd chapter of the excellent book Arithmétique des ordinateurs by Jean-Michel Muller (in French).
1. A. Avizienis. Signed-digit number representations for fast parallel arithmetic. IRE Transactions on electronic computers, vol 10, pages 389-400, 1961This operation computes Z ← X+Y. As we said earlier, the redundant number representation can "absorb" the carry in the next word without propagating it. This is the original Avizienis algorithm:
si = Xi + Yi if • si ≤ -M: Ti+1 = -1 and Si = si + B • -M < si < M: Ti+1 = 0 and Si = si • M ≤ si: Ti+1 = 1 and Si = si - B Zi = Si + Ti
The "carry" vector Ti depends on the input digits at rank i-1 only, and can be computed in parallel for all words. T0 is 0, and TN is the output "carry" (dropped).
The max values of Xi and Yi are both M, so si has a max value of 2M, and the max value for Zi is 2M+1-B, which must be ≤M to maintain the range of the digits. Solving this, we obtain the conditions M<B<2M for the original Avizienis algorithm. Additionally, the value 2M must fit on a signed machine word. With 32-bit words, we must take M<230, and M<262 with 64-bit words.
Simplified version
To simplify, we will restrict ourselves to positive values in range 0..M, representing only non negative integers, and assume B is a power of 2. Then the following algorithm works without branches:
si = Xi + Yi Ti+1 = si >> LOGBASE // bitwise shift, B is 2LOGBASE Si = si & (BASE-1) // bitwise and Zi = Si + Ti
M must verify M>B for this algorithm to maintain the bounds on output. The smallest valid value is M=B+1, and since 2M must fit on an unsigned machine word, we get B=230 for 32-bit words, and B=262 for 64-bit words.
GPU kernel
This kernel implements the simplified algorithm:
// ADD v1
__kernel void add_v1(__global const Word * x,__global const Word * y,__global Word * z)
{
int i = get_global_id(0);
// Carry from I-1
Word t = (Word)0;
if (i>0)
{
t = (x[i-1]+y[i-1]) >> LOG_BASE;
}
// Sum I
Word s = (x[i]+y[i]) & BASE_MINUS1;
// Final result
z[i] = t + s;
}
CPU code
The CPU code is almost identical to the GPU kernel. The difference is that each CPU thread computes a block of contiguous digits, instead of one single digit for the GPU kernel.
template <typename T,int LOG_BASE> void addNv1(AddNThreadParam * p)
{
size_t n = p->sz / sizeof(T); // Words in block
const T * a = (const T *)(p->a);
const T * b = (const T *)(p->b);
T * out = (T *)(p->out);
T BASE = (T)1<<(T)LOG_BASE;
T BASE_MINUS1 = BASE - (T)1;
T t = 0; // "carry" from previous word
if (p->index > 0)
{
// Get "carry" for last values of previous block
t = (a[-1] + b[-1]) >> (T)LOG_BASE;
}
for (size_t i=0;i<n;i++)
{
T s = a[i] + b[i];
out[i] = (s & BASE_MINUS1) + t;
t = s >> (T)LOG_BASE;
}
}
Measured throughput
The throughput is measured in MB of result per second. The measured values are lowered to take into account that we compute only 14, 30, 62 bits for resp. 16, 32, 64 bit words.
The measured timings are shown in the following graphs, for various word sizes: 16, 32, and 64 bits. The Windows 64-bit ATI driver does not provide valid measures, and they were omitted. I will update the curves as soon as ATI releases a better driver.
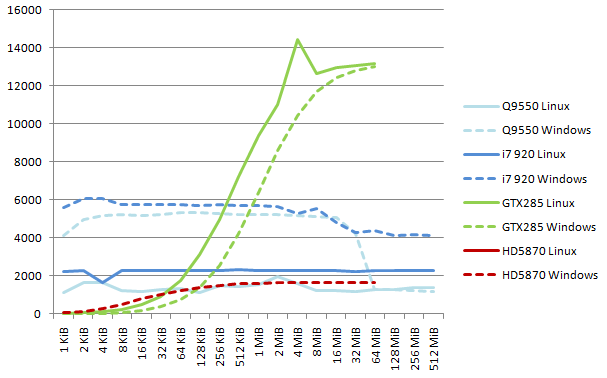
Note on 16-bit results. The Linux CPU code generated by gcc is clearly not optimized for 16-bit words, and runs at half speed with respect to the Visual Studio code. The ATI driver requires enabling the cl_khr_byte_addressable_store extension to compile the kernel. The best CPU reaches 6.0 GB/s; the GTX285 reaches 14.4 GB/s and the HD5870 1.6 GB/s (from 6.6 GB/s with SDK 2.01).
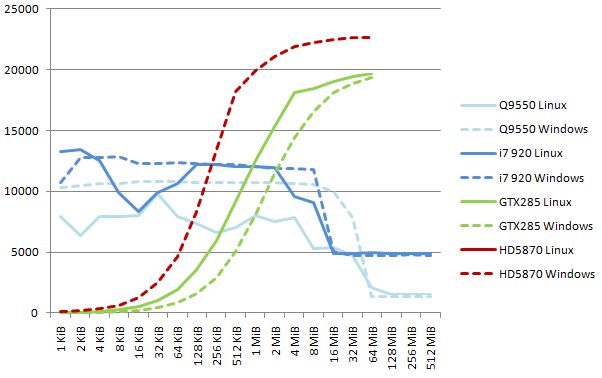
Note on 32-bit results. The patterns here are more regular, except a gap in Linux CPU performance around 16 KiB data size. Since the code runs normally otherwise, the gap must come from the Linux kernel itself, and be related to memory and/or thread management and how they interact with the CPU cache. CPU performance is stable at 12 GB/s for blocks up to 8 MiB. The GTX285 reaches a top speed of 19.6 GB/s and the HD5870 reaches 22.6 GB/s (from 11.7 GB/s with SDK 2.01).
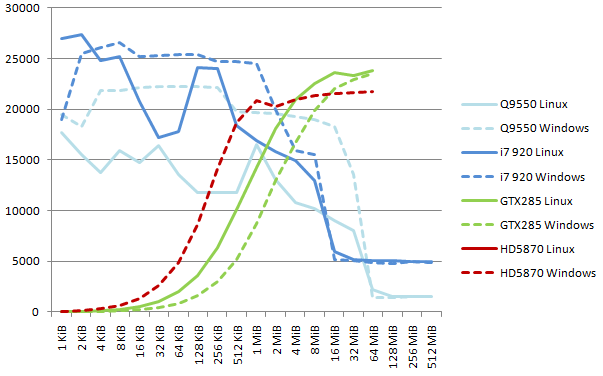
Note on 64-bit results. The patterns are identical to the 32-bit curves. CPU performance for low block size (less than 4 MiB) nearly doubles, from 12 to 25 GB/s. GPU performance raises in a lower proportion, and reaches 23 GB/s for the GTX285 and 21.7 GB/s (from 16.7 GB/s with SDK 2.01) for the HD5870.
On the Core i7, 64-bit single-thread addition with carry propagation runs at 2.25 cycles per word (GMP) with data in the L1 cache. At 3.3GHz, it corresponds to 11.7 GB/s for GMP.
Generally, the redundant notation allows multithreading, and provides a large improvement (2x) over GMP, and it could be made even larger by folding the numbers into 4 interleaved parts, and processing them with vector instructions, 4*32-bits or 2*64-bits at a time. The GPU are more interesting than the CPU outside the limits of the CPU cache system, for blocks larger than 16 MiB.
As a proof of concept, I measured the speed of the following SSE code, computing almost the correct sum, with the exception of the first values of each block:
void addNv3(AddNThreadParam * p)
{
const int LOG_BASE = 30;
const int BASE = 1<sz >> 4; // We process blocks of 16 bytes
const __m128i * a = (const __m128i *)(p->a);
const __m128i * b = (const __m128i *)(p->b);
__m128i * out = (__m128i *)(p->out);
__m128i mask = _mm_set1_epi32(BASE_MINUS1);
__m128i t = _mm_setzero_si128();
// TODO: initialize T with the correct values from the end of previous block
for (size_t i=0;i<n;i++)
{
__m128i s = _mm_add_epi32(_mm_load_si128(a+i),_mm_load_si128(b+i));
__m128i o = _mm_add_epi32(_mm_and_si128(s,mask),t);
_mm_store_si128(out+i,o);
t = _mm_srli_epi32(s,LOG_BASE);
}
}
This code operates on vectors of four 32-bit values (16 bytes). On the Core i7, the measured top speed is 47 GB/s, a little more than 4x the GMP or MPIR speed. The digits need to be interleaved in memory: the first quarter of the digits at offsets 0,4,8,... the second quarter at offsets 1,5,9,... and so on. At this speed, the CPU runs at nearly 100%: the body of the loop executes in 4 cycles, as required by 2*add+1*and+1*srl.
Before experimenting on less memory-limited operations, let's measure in the next section the raw arithmetic power available on the CPU and the GPU.
| GPU Benchmarks : Memory operations | Top of Page | GPU Benchmarks : Available Flops |
