How fast can we compute 1D gradient?

Eric Bainville - Oct 2009

SSE vector right shift

In this section, we are looking for the most efficient solution to shift a float in[n] vector right by one element. The output float out[n] is defined as:

out[0] = 0
out[i] = in[i-1] if i>0

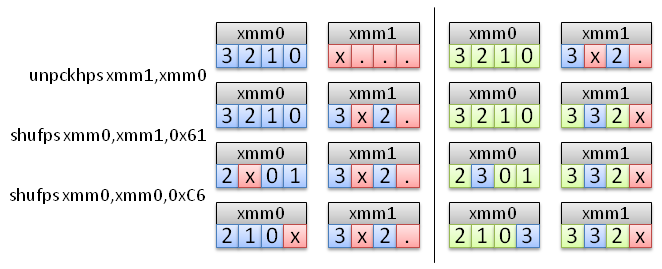
The puzzle is to use the SSE instructions of the previous page to shift the vector. After trying "by hand" for a few hours, I gave up and wrote a small program to check all sequences of instructions. The results are quite interesting: at least 3 instructions are needed (excluding the memory load and store) and there are only 4 solutions using 3 instructions. Here are the four solutions, the input is in xmm0, and the output too.

unpckhps xmm1,xmm0
shufps   xmm0,xmm1,0x61
shufps   xmm0,xmm0,0xC6

unpckhps xmm1,xmm0
shufps   xmm0,xmm1,0x64
shufps   xmm0,xmm0,0xD2

unpckhps xmm1,xmm0
shufps   xmm0,xmm1,0x91
shufps   xmm0,xmm0,0x87

unpckhps xmm1,xmm0
shufps   xmm0,xmm1,0x94
shufps   xmm0,xmm0,0x93

Two iterations of the first solution. The blue vector is loaded from memory in the first iteration, and the green vector is loaded in the second iteration. The other solutions are trivial variants of this one.

Instead of an __asm block with assembly instructions, we will use the SSE intrinsics. The corresponding code is:

__m128 r0,r1;
r1 = _mm_setzero_ps();
for (int i=(n>>2);i>0;i--)
{
  r0 = _mm_load_ps(in);
  in += 4;
  r1 = _mm_unpackhi_ps(r1,r0);
  r0 = _mm_shuffle_ps(r0,r1,0x61);
  r0 = _mm_shuffle_ps(r0,r0,0xC6);
  _mm_store_ps(out,r0);
  out += 4;
}

It runs at 1.0 cycles/float. Unrolling the loop to process 8 floats per iteration, we reach 0.9 cycles/float. The three unpack/shuffle instructions all use the same execution port of the processor, so the best execution time is at least 0.75 cycles/float.

With this code already running at 1.0 cycles/float and the C code running at 1.6 cycles/float, it is very unlikely we will be able to compute the corresponding left shift and the subtraction in 0.6 additional cycles/float. Using SSE to compute a single line gradient is probably not better than the C code. However, we may have more luck by computing the gradient of 4 vectors in parallel.

We need to work on blocks of 4x4 pixels:

Load one block (4 movaps).
Transpose it (8 shufps).
Compute the gradient (4 subps).
Transpose the block again (8 shufps).
Store the block (4 movaps).

This sequence must be adapted to finish computation and store the previous block after the next one is loaded, because we need its first column to compute the last column of the previous block.

After various attempts, the best I could reach was 1.9 cycles/float. The load/transpose/store operation runs at 0.83 cycles/float, giving an estimate of 2.1 cycles/float for first computing the transpose and storing it in place, then compute the gradient, and transposing again.