GPU matrix-vector product (gemv)

P threads per dot product

In this new version, we will run mxp threads in a 2-dimensional range. Dimension 0 corresponds to the m rows of the matrix, and dimension 1 contains p threads, each of them computing one section of the dot product.

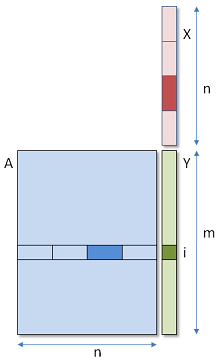
In a single row i, the p threads need to communicate to compute the sum of their respective contributions to Y_i. This implies that they must belong to the same work group, and share some local memory.

To simplify the loop, the dot product is computed in each thread for columns k=k₀+p*i instead of blocks of consecutive columns. The kernel is the following:

#define ROW_DIM 0
#define COL_DIM 1
// P threads per row compute 1/P-th of each dot product.
// WORK has P columns and get_local_size(0) rows.
__kernel void gemv2(__global const scalar_t * a,
                    __global const scalar_t * x,
		    __global scalar_t * y,
		    __local scalar_t * work,
		    int m,int n)
{
  // Compute partial dot product
  scalar_t sum = (scalar_t)0;
  for (int k=get_global_id(COL_DIM);k<n;k+=get_global_size(COL_DIM))
    {
      sum += a[get_global_id(ROW_DIM)+m*k] * x[k];
    }

  // Each thread stores its partial sum in WORK
  int rows = get_local_size(ROW_DIM); // rows in group
  int cols = get_local_size(COL_DIM); // initial cols in group
  int ii = get_local_id(ROW_DIM); // local row index in group, 0<=ii<rows
  int jj = get_local_id(COL_DIM); // block index in column, 0<=jj<cols
  work[ii+rows*jj] = sum;
  barrier(CLK_LOCAL_MEM_FENCE); // sync group

  // Reduce sums in log2(cols) steps
  while ( cols > 1 )
    {
      cols >>= 1;
      if (jj < cols) work[ii+rows*jj] += work[ii+rows*(jj+cols)];
      barrier(CLK_LOCAL_MEM_FENCE); // sync group
    }

  // Write final result in Y
  if ( jj == 0 ) y[get_global_id(ROW_DIM)] = work[ii];
}

The barrier calls are required to ensure all threads in the work group have written their sums into the local work array before reading them in other threads of the group.

Exchanging ROW_DIM and COL_DIM leads to a huge performance drop, because the broadcast access to x[k] occurs only when the threads are executed in the same warp/wavefront. For the NVidia devices, warps are clearly built from threads in dimension 0, then dimension 1. The OpenCL standard doesn't specify anything about the basic scheduling units (warps/wavefronts), and the mapping between work items and the physical warps/wavefronts.

The best measured timings are the following:

GTX285, v2, float:  M = 74 GB/s  C = 37 GFlops  (P=4 M'=64)
HD5870, v2, float:  M = 61 GB/s  C = 30 GFlops  (P=4 M'=64)

GTX285, v2, double: M = 83 GB/s  C = 21 GFlops  (P=4 M'=32)
HD5870, v2, double: M = 93 GB/s  C = 23 GFlops  (P=8 M'=32)

The single precision kernel runs 1.5x faster than CUBLAS in this case, and the double precision kernel is still 10% behind CUBLAS.

In the next page, we will load in local memory the part of X used by all threads in the block.