GPU matrix-vector product (gemv)
Eric Bainville - Feb 2010Two kernels
We now run p threads per row, but each thread will preload the corresponding portion of X in local memory, to make it available to all threads of the group. The result will be stored in global memory in a mxp matrix, and reduced in another kernel. When p is small enough, the cost of the reduction is negligible compared to the computation of all partial sums.
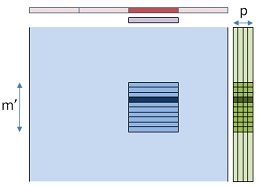
Here is the code of the two kernels:
// P threads per row compute 1/P-th of each dot product. // WORK has N/P entries. __kernel void gemv3(__global const scalar_t * a,__global const scalar_t * x, __global scalar_t * y, __local scalar_t * work, int m,int n) { // Load a slice of X in WORK, using all available threads int ncols = n / get_global_size(COL_DIM); // nb values to load int col0 = ncols * get_global_id(COL_DIM); // first value to load for (int k=0;k<ncols;k+=get_local_size(ROW_DIM)) { int col = k+get_local_id(ROW_DIM); if (col < ncols) work[col] = x[col0+col]; } barrier(CLK_LOCAL_MEM_FENCE); // sync group // Compute partial dot product scalar_t sum = (scalar_t)0; for (int k=0;k<ncols;k++) { sum += a[get_global_id(ROW_DIM)+m*(col0+k)] * work[k]; } // Store in Y (P columns per row) y[get_global_id(ROW_DIM)+m*get_global_id(COL_DIM)] = sum; } // Reduce M = get_global_size(0) rows of P values in matrix Y. // Stores the result in first column of Y. __kernel void reduce_rows(__global scalar_t * y,int m,int p) { int row = get_global_id(0); scalar_t sum = (scalar_t)0; for (int col=0;col<p;col++) sum += y[row + m*col]; y[row] = sum; }
The best measured timings are the following:
GTX285, v3, float: M = 124 GB/s C = 62 GFlops (P=4 M'=256) HD5870, v3, float: M = 82 GB/s C = 41 GFlops (P=32 M'=256) GTX285, v3, double: M = 105 GB/s C = 26 GFlops (P=16 M'=128) HD5870, v3, double: M = 128 GB/s C = 32 GFlops (P=64 M'=256)
In this version, the requirements in local memory for each group are smaller (n/p scalars), allowing more groups to run concurrently in each stream processor. Another advantage is we can maximize the reuse of the X slices copied to local memory, because the work group width is now 1 thread only (we don't need all threads affected to the same row to communicate), and we can assign the total work group capacity (256 threads for ATI and 512 threads for NVidia) to the computation of rows.
The single precision gemv runs at a nice 2.6x CUBLAS speed, and we got a smaller 16% gain over the CUBLAS speed in double precision.
Replacing the sum += a[...] * work[k] instruction by a call to the OpenCL built-in functions sum = fma(a[...],work[k],sum) and sum = mad(a[...],work[k],sum) gives the following results:
fma: GTX285, v3, float: M = 12 GB/s C = 6 GFlops (P=32 M'=64) HD5870, v3, float: M = 12 GB/s C = 6 GFlops (P=32 M'=256) GTX285, v3, double: M = 108 GB/s C = 27 GFlops (P=16 M'=64) HD5870, v3, double: build failed mad: GTX285, v3, float: M = 124 GB/s C = 62 GFlops (P=4 M'=256) HD5870, v3, float: M = 82 GB/s C = 41 GFlops (P=32 M'=256) GTX285, v3, double: M = 108 GB/s C = 27 GFlops (P=16 M'=64) HD5870, v3, double: build failed
There is almost no improvement, and fma introduces a huge performance drop when used on float (on both devices). Only the double+mad variant brings a little 3% of performance in the case of the GTX285.
In the next page, let's put together a few concluding remarks on this study.
| OpenCL GEMV : P threads per dot product | Top of Page | OpenCL GEMV : Conclusions |
