OpenCL Fast Fourier Transform
Eric Bainville - May 2010One work-group per DFT (2)
In this page, instead of storing the DFT arguments in local memory, we will store them directly in registers inside each thread, and use local memory to exchange values between threads.
Example: one DFT4 per thread
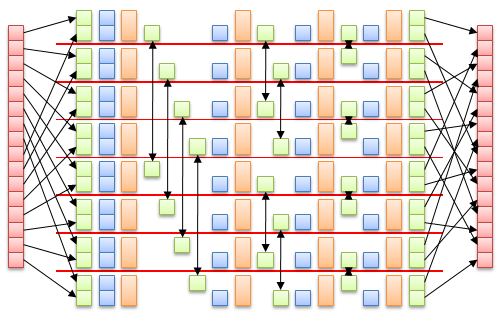
In this example, we will compute one DFT4 per thread, operating in-place on 4 registers. All T threads of each work-group will be used together to compute a DFT4T. Shared memory for the work-group will be used to transfer values between threads. Each kernel of G groups will compute G × DFT4T, with initial input from global memory, and final output to global memory. N=4.T.G is the size of the top-level DFT.
Let's decompose the work of a work-group. It operates on an initial sequence x0[0] of length 4.n0, where n0=T.
During the first step of the computation, thread t (t=0..T-1) will load (from global memory) and "twiddle" four values of x0[0] at indices i, i+n0, i+2.n0, i+3.n0, where i is an index in range 0..n0-1 computed from t. The thread will then compute their DFT4, and own the result: the four values at indices i in the 4 sequences x1[0], x1[1], x1[2], x1[3]. These sequences have length 4.n1, where n1=n0/4.
In the second step, thread t will operate on four values at indices j, j+n1, j+2.n1, j+3.n1 in sequence x1[k], where j in 0..n1-1 and k in 0..3 are computed from t. The 4 inputs have to be obtained and twiddled from the thread currently owning them. The 4 outputs are elements at index j in sequences x2[k], x2[k+4], x2[k+8], x2[k+12].
The process terminates when the length of the sequences reach 1 (T must be a multiple of 4). We have full freedom in the choice of the mapping (sequence id,index) → thread id for each level.
Implementing one DFT2 per thread
Here each thread will compute successive DFT2 on 2 registers. After a few experiments, I have found a pattern allowing this with only one read+write in local memory per thread between successive DFT2
// pow_theta(p,q) returns exp(-Pi*P/Q) // revbits(p,i) returns i with the lower log2(p) bits reversed, p is a power of 2 // DFT2(a,b) replaces (a,b) with (a+b,a-b) // mul_minus_i(a) returns (a.y,-a.x) // X[N], Y[N], U[LOCAL_SIZE], P is the input sequence length, initially 1, and // multiplied by 2*LOCAL_SIZE at each kernel invocation. __kernel void fft_s2(__global const float2 * x,__global float2 * y,__local float2 * u,int p) { int i = get_local_id(0); // current thread in group, in 0..LOCAL_SIZE-1 int irev = revbits(LOCAL_SIZE,i); // reverse binary of I int k = get_group_id(0)&(p-1); // index in input sequence, in 0..P-1 float2 twiddle; float2 r0,r1; // Load and twiddle 2 values in registers r0 = x[get_group_id(0) + i * get_num_groups(0)]; twiddle = pow_theta(k*i,LOCAL_SIZE*p); r0 = mul(r0,twiddle); r1 = x[get_group_id(0) + (i+LOCAL_SIZE) * get_num_groups(0)]; twiddle = pow_theta(k*(i+LOCAL_SIZE),LOCAL_SIZE*p); r1 = mul(r1,twiddle); // Compute DFT_{2*LOCAL_SIZE} in group DFT2(r0,r1); twiddle = (float2)(1,0); for (int bit=LOCAL_SIZE>>1;bit>0;bit>>=1) { // Write u[i] = (i&bit)?r0:r1; barrier(CLK_LOCAL_MEM_FENCE); // Read float2 aux = u[i^bit]; barrier(CLK_LOCAL_MEM_FENCE); if (i&bit) r0 = aux; else r1 = aux; // Twiddle twiddle = normalize(twiddle + (float2)(1,0)); // half angle twiddle = (i&bit)?mul_minus_i(twiddle):twiddle; r1 = mul(r1,twiddle); // DFT2 DFT2(r0,r1); } // Store result int j = (get_group_id(0)-k)*2*LOCAL_SIZE+k; // index in output sequence y[j+irev*p] = r0; y[j+(irev+LOCAL_SIZE)*p] = r1; }
Here again, the global memory read and write patterns kill the performance:
| Group size | GTX285 | HD5870 |
|---|---|---|
| 128 | 681 ms | 845 ms |
The table below gives an idea of the code bottlenecks:
| Operation | GTX285 | HD5870 |
|---|---|---|
| All code enabled | 681 ms | 845 ms |
| A. Irregular x read replaced with coalesced | 198 ms | 404 ms |
| B. Irregular y write replaced with coalesced | 505 ms | 638 ms |
| A and B | 38 ms | 32 ms |
| C. Initial x twiddle disabled | 722 ms | 679 ms |
| A and B and C | 32 ms | 24 ms |
| D. Local memory exchanges disabled | 569 ms | 843 ms |
| A and B and C and D | 21 ms | 20 ms |
Only the first row corresponds to an actual computation of the DFT.
Implementing one DFTp per thread
The pattern presented above can be extended to arbitrary size DFT, keeping one float2 per thread in local memory for transferts. The first timings obtained show no improvement in running time.
To be continued...
| OpenCL FFT (OLD) : One work-group per DFT (1) | Top of Page | OpenCL GEMV |
