OpenCL Fast Fourier Transform
Eric Bainville - May 2010Higher radix kernels
Radix-4 kernel
We will now merge two consecutive iterations. Two iterations of the FFT radix-2 algorithm will combine 4 sub-sequences of length p into one sequence of length 4p, corresponding to a "radix-4" algorithm.
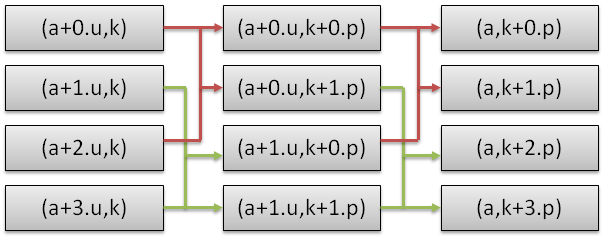
The radix-4 butterfly simplifies to a length 4 DFT applied on scaled inputs (a+0.u,k)p, (a+1.u,k)p * ω1, (a+2.u,k)p * ω2, and (a+3.u,k)p * ω3, where ω=e-2*π*i/(2p).
First, we have to define the following new functions:
// Return a*EXP(-I*PI*1/2) = a*(-I) float2 mul_p1q2(float2 a) { return (float2)(a.y,-a.x); } // Return a^2 float2 sqr_1(float2 a) { return (float2)(a.x*a.x-a.y*a.y,2.0f*a.x*a.y); } // Return the 2x DFT2 of the four complex numbers in A // If A=(a,b,c,d) then return (a',b',c',d') where (a',c')=DFT2(a,c) // and (b',d')=DFT2(b,d). float8 dft2_4(float8 a) { return (float8)(a.lo+a.hi,a.lo-a.hi); } // Return the DFT of 4 complex numbers in A float8 dft4_4(float8 a) { // 2x DFT2 float8 x = dft2_4(a); // Shuffle, twiddle, and 2x DFT2 return dft2_4((float8)(x.lo.lo,x.hi.lo,x.lo.hi,mul_p1q2(x.hi.hi))); }
We implemented several versions of the radix-4 kernel:
// T = N/4 = number of threads. // P is the length of input sub-sequences, 1,4,16,...,N/4. __kernel void fft_radix4(__global const float2 * x,__global float2 * y,int p) { int t = get_global_size(0); // number of threads int i = get_global_id(0); // current thread int k = i & (p-1); // index in input sequence, in 0..P-1 // Inputs indices are I+{0,1,2,3}*T x += i; // Output indices are J+{0,1,2,3}*P, where // J is I with two 0 bits inserted at bit log2(P) y += ((i-k)<<2) + k; // Load and twiddle inputs // Twiddling factors are exp(_I*PI*{0,1,2,3}*K/2P) float alpha = -M_PI*(float)k/(float)(2*p); [VARIANT CODE] }
Variant A, working with float2 numbers:
// Load and twiddle float2 u0 = x[0]; float2 u1 = mul_1(exp_alpha_1(alpha),x[t]); float2 u2 = mul_1(exp_alpha_1(2*alpha),x[2*t]); float2 u3 = mul_1(exp_alpha_1(3*alpha),x[3*t]); // 2x DFT2 and twiddle float2 v0 = u0 + u2; float2 v1 = u0 - u2; float2 v2 = u1 + u3; float2 v3 = mul_p1q2(u1 - u3); // twiddle // 2x DFT2 and store y[0] = v0 + v2; y[p] = v1 + v3; y[2*p] = v0 - v2; y[3*p] = v1 - v3;
Variant B, working with float8 numbers and the dft4_4 function:
// Load, and DFT4 float8 u = dft4_4( (float8)( x[0], mul_1(exp_alpha_1(alpha),x[t]), mul_1(exp_alpha_1(2*alpha),x[2*t]), mul_1(exp_alpha_1(3*alpha),x[3*t]) )); // Store y[0] = u.lo.lo; y[p] = u.lo.hi; y[2*p] = u.hi.lo; y[3*p] = u.hi.hi;
And variant C: variant A where the 3 calls to exp_alpha and 3 mul are replaced with one single call to exp_alpha and 5 mul:
// Load and twiddle, one exp_alpha computed instead of 3 float2 twiddle = exp_alpha_1(alpha); float2 u0 = x[0]; float2 u1 = mul_1(twiddle,x[t]); float2 u2 = x[2*t]; float2 u3 = mul_1(twiddle,x[3*t]); twiddle = sqr_1(twiddle); u2 = mul_1(twiddle,u2); u3 = mul_1(twiddle,u3); // 2x DFT2 and twiddle float2 v0 = u0 + u2; float2 v1 = u0 - u2; float2 v2 = u1 + u3; float2 v3 = mul_p1q2(u1 - u3); // twiddle // 2x DFT2 and store y[0] = v0 + v2; y[p] = v1 + v3; y[2*p] = v0 - v2; y[3*p] = v1 - v3;
log2(N)/2 iterations each running N/4 threads are required. I measured the best time (among all work-group sizes) for all 3 variants of the kernel and all 3 variants of the cos+sin computation:
| Radix-4 | GTX285 | HD5870 | ||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| sincos | 38 ms | 37 ms | 31 ms | 33 ms | 34 ms | 38 ms |
| sin+cos | 33 ms | 32 ms | 31 ms | 51 ms | 51 ms | 39 ms |
| native sin+cos | 33 ms | 32 ms | 31 ms | 38 ms | 39 ms | 38 ms |
For the NVidia GTX285, the best performance (green cells) is obtained when computing only one cos+sin instead of three, independently of the cos+sin computation variant. On the HD5870, the best performance (red cell) is reached while working on float2 numbers, and using sincos to compute cos+sin. On the ATI GPU, the native cos+sin is slightly slower, and the precise cos+sin is really slow.
Radix-8 kernel
Pushing further this idea, we can implement a radix-8 kernel. Let's first define the required functions:
// mul_p*q*(a) returns a*EXP(-I*PI*P/Q) #define mul_p0q1(a) (a) #define mul_p0q2 mul_p0q1 float2 mul_p1q2(float2 a) { return (float2)(a.y,-a.x); } __constant float SQRT_1_2 = 0.707106781188f; // cos(Pi/4) #define mul_p0q4 mul_p0q2 float2 mul_p1q4(float2 a) { return (float2)(SQRT_1_2)*(float2)(a.x+a.y,-a.x+a.y); } #define mul_p2q4 mul_p1q2 float2 mul_p3q4(float2 a) { return (float2)(SQRT_1_2)*(float2)(-a.x+a.y,-a.x-a.y); }
Then, the radix-8 kernel is:
// T = N/8 = number of threads. // P is the length of input sub-sequences, 1,8,64,...,N/8. __kernel void fft_radix8(__global const float2 * x,__global float2 * y,int p) { int t = get_global_size(0); // number of threads int i = get_global_id(0); // current thread int k = i & (p-1); // index in input sequence, in 0..P-1 // Inputs indices are I+{0,1,2,3,4,5,6,7}*T x += i; // Output indices are J+{0,1,2,3,4,5,6,7}*P, where // J is I with three 0 bits inserted at bit log2(P) y += ((i-k)<<3) + k; // Load and twiddle inputs // Twiddling factors are exp(_I*PI*{0,1,2,3,4,5,6,7}*K/4P) float alpha = -M_PI*(float)k/(float)(4*p); // Load and twiddle {VARIANT CODE] // 4x in-place DFT2 and twiddle float2 v0 = u0 + u4; float2 v4 = mul_p0q4(u0 - u4); float2 v1 = u1 + u5; float2 v5 = mul_p1q4(u1 - u5); float2 v2 = u2 + u6; float2 v6 = mul_p2q4(u2 - u6); float2 v3 = u3 + u7; float2 v7 = mul_p3q4(u3 - u7); // 4x in-place DFT2 and twiddle u0 = v0 + v2; u2 = mul_p0q2(v0 - v2); u1 = v1 + v3; u3 = mul_p1q2(v1 - v3); u4 = v4 + v6; u6 = mul_p0q2(v4 - v6); u5 = v5 + v7; u7 = mul_p1q2(v5 - v7); // 4x DFT2 and store (reverse binary permutation) y[0] = u0 + u1; y[p] = u4 + u5; y[2*p] = u2 + u3; y[3*p] = u6 + u7; y[4*p] = u0 - u1; y[5*p] = u4 - u5; y[6*p] = u2 - u3; y[7*p] = u6 - u7; }
Variant A of the load and twiddle code computes cos+sin 7 times, and 7 complex number products:
// Load and twiddle (variant A) float2 u0 = x[0]; float2 u1 = mul_1(exp_alpha_1(alpha),x[t]); float2 u2 = mul_1(exp_alpha_1(2*alpha),x[2*t]); float2 u3 = mul_1(exp_alpha_1(3*alpha),x[3*t]); float2 u4 = mul_1(exp_alpha_1(4*alpha),x[4*t]); float2 u5 = mul_1(exp_alpha_1(5*alpha),x[5*t]); float2 u6 = mul_1(exp_alpha_1(6*alpha),x[6*t]); float2 u7 = mul_1(exp_alpha_1(7*alpha),x[7*t]);
Variant B of the load and twiddle block uses only 1 cos+sin call, and computes the remaining twiddle factors using 14 complex number products. As we have seen above, it should run faster on the GTX285.
// Load and twiddle (variant B) float2 twiddle = exp_alpha_1(alpha); // W float2 u0 = x[0]; float2 u1 = mul_1(twiddle,x[t]); float2 u2 = x[2*t]; float2 u3 = mul_1(twiddle,x[3*t]); float2 u4 = x[4*t]; float2 u5 = mul_1(twiddle,x[5*t]); float2 u6 = x[6*t]; float2 u7 = mul_1(twiddle,x[7*t]); twiddle = sqr_1(twiddle); // W^2 u2 = mul_1(twiddle,u2); u3 = mul_1(twiddle,u3); u6 = mul_1(twiddle,u6); u7 = mul_1(twiddle,u7); twiddle = sqr_1(twiddle); // W^4 u4 = mul_1(twiddle,u4); u5 = mul_1(twiddle,u5); u6 = mul_1(twiddle,u6); u7 = mul_1(twiddle,u7);
As in the radix-4 kernels, I measured the best execution time for the two variants of the code and the three variants of cos+sin computation:
| Radix-8 | GTX285 | HD5870 | ||
|---|---|---|---|---|
| A | B | A | B | |
| sincos | 40 ms | 30 ms | 25 ms | 30 ms |
| sin+cos | 31 ms | 30 ms | 40 ms | 29 ms |
| native sin+cos | 31 ms | 30 ms | 29 ms | 29 ms |
The GTX285 performance remains comparable to kernel-4 performance. On the HD5870 side, we observe a nice improvement. Let's continue in the same spirit with a radix-16 kernel.
Radix-16 kernel
Extension to radix-16 is straightforward. First define the twiddling functions, and a combined DFT2+twiddle macro:
__constant float COS_8 = 0.923879532511f; // cos(Pi/8) __constant float SIN_8 = 0.382683432365f; // sin(Pi/8) #define mul_p0q8 mul_p0q4 float2 mul_p1q8(float2 a) { return mul_1((float2)(COS_8,-SIN_8),a); } #define mul_p2q8 mul_p1q4 float2 mul_p3q8(float2 a) { return mul_1((float2)(SIN_8,-COS_8),a); } #define mul_p4q8 mul_p2q4 float2 mul_p5q8(float2 a) { return mul_1((float2)(-SIN_8,-COS_8),a); } #define mul_p6q8 mul_p3q4 float2 mul_p7q8(float2 a) { return mul_1((float2)(-COS_8,-SIN_8),a); } // Compute in-place DFT2 and twiddle #define DFT2_TWIDDLE(a,b,t) { float2 tmp = t(a-b); a += b; b = tmp; }
Then the radix-16 kernel is the following. We used an array of registers, in the hope the compiler would handle it correctly. Fixed-size arrays and loops are OK; but in some other cases, the private array may be physically located in global memory, annihilating kernel performance.
// T = N/16 = number of threads. // P is the length of input sub-sequences, 1,16,256,...,N/16. __kernel void fft_radix16(__global const float2 * x,__global float2 * y,int p) { int t = get_global_size(0); // number of threads int i = get_global_id(0); // current thread int k = i & (p-1); // index in input sequence, in 0..P-1 // Inputs indices are I+{0,..,15}*T x += i; // Output indices are J+{0,..,15}*P, where // J is I with four 0 bits inserted at bit log2(P) y += ((i-k)<<4) + k; // Load float2 u[16]; for (int m=0;m<16;m++) u[m] = x[m*t]; // Twiddle, twiddling factors are exp(_I*PI*{0,..,15}*K/4P) float alpha = -M_PI*(float)k/(float)(8*p); for (int m=1;m<16;m++) u[m] = mul_1(exp_alpha_1(m*alpha),u[m]); // 8x in-place DFT2 and twiddle (1) DFT2_TWIDDLE(u[0],u[8],mul_p0q8); DFT2_TWIDDLE(u[1],u[9],mul_p1q8); DFT2_TWIDDLE(u[2],u[10],mul_p2q8); DFT2_TWIDDLE(u[3],u[11],mul_p3q8); DFT2_TWIDDLE(u[4],u[12],mul_p4q8); DFT2_TWIDDLE(u[5],u[13],mul_p5q8); DFT2_TWIDDLE(u[6],u[14],mul_p6q8); DFT2_TWIDDLE(u[7],u[15],mul_p7q8); // 8x in-place DFT2 and twiddle (2) DFT2_TWIDDLE(u[0],u[4],mul_p0q4); DFT2_TWIDDLE(u[1],u[5],mul_p1q4); DFT2_TWIDDLE(u[2],u[6],mul_p2q4); DFT2_TWIDDLE(u[3],u[7],mul_p3q4); DFT2_TWIDDLE(u[8],u[12],mul_p0q4); DFT2_TWIDDLE(u[9],u[13],mul_p1q4); DFT2_TWIDDLE(u[10],u[14],mul_p2q4); DFT2_TWIDDLE(u[11],u[15],mul_p3q4); // 8x in-place DFT2 and twiddle (3) DFT2_TWIDDLE(u[0],u[2],mul_p0q2); DFT2_TWIDDLE(u[1],u[3],mul_p1q2); DFT2_TWIDDLE(u[4],u[6],mul_p0q2); DFT2_TWIDDLE(u[5],u[7],mul_p1q2); DFT2_TWIDDLE(u[8],u[10],mul_p0q2); DFT2_TWIDDLE(u[9],u[11],mul_p1q2); DFT2_TWIDDLE(u[12],u[14],mul_p0q2); DFT2_TWIDDLE(u[13],u[15],mul_p1q2); // 8x DFT2 and store (reverse binary permutation) y[0] = u[0] + u[1]; y[p] = u[8] + u[9]; y[2*p] = u[4] + u[5]; y[3*p] = u[12] + u[13]; y[4*p] = u[2] + u[3]; y[5*p] = u[10] + u[11]; y[6*p] = u[6] + u[7]; y[7*p] = u[14] + u[15]; y[8*p] = u[0] - u[1]; y[9*p] = u[8] - u[9]; y[10*p] = u[4] - u[5]; y[11*p] = u[12] - u[13]; y[12*p] = u[2] - u[3]; y[13*p] = u[10] - u[11]; y[14*p] = u[6] - u[7]; y[15*p] = u[14] - u[15]; }
| Radix-16 | GTX285 | HD5870 |
|---|---|---|
| sincos | 46 ms | 29 ms |
| sin+cos | 45 ms | 38 ms |
| native sin+cos | 45 ms | 18 ms |
Things are becoming quite interesting here: the HD5870 beats the performance of CUBLAS! Strangely, the native sin+cos is now faster than sincos. Each kernel continues to execute in 3 ms despite the increased computation load. Juste to see how far it can go before the number of registers becomes a limiting factor, let's implement a radix-32 kernel.
Radix-32 kernel
The problem with the radix-32 kernel is how we can test it: we can't allocate larger buffers on the HD5870, so we are limited to N=224, and 24 is not a multiple of 5. So we will have to call 4x radix-32 and 1x radix-16 to reach 24.
The code for the radix-32 kernel is a trivial evolution from the previous ones. We get the following running times:
| Radix-32 | GTX285 | HD5870 |
|---|---|---|
| sincos | 45 ms | 34 ms |
| sin+cos | 41 ms | 44 ms |
| native sin+cos | 41 ms | 22 ms |
We see the radix-32 kernel uses too many resources, limiting the performances. In the following page, we will benchmark the radix-r kernels: Radix-r kernels benchmarks.
| OpenCL FFT (OLD) : Radix-2 kernel | Top of Page | OpenCL FFT (OLD) : Radix-r kernels benchmarks |
